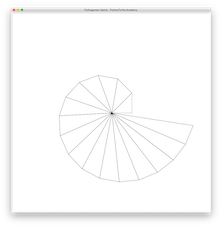
Also known as Spiral of Theodorus, this spiral draws a series of side by side right triangles with one leg having fixed unit size, and the other leg a series
Day: March 8, 2019
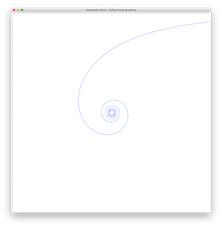
Hyperbolic SpiralHyperbolic Spiral
Also known as reciprocal spiral, it is an inverse of Archimedean spiral. This means the radius grows in proportion to the inverse of angle. To avoid infinite radius, start with

Growing Vogel’s Model AnimationGrowing Vogel’s Model Animation
Animate the colored Vogel’s Model by showing it growing.

Vogel’s Model with ColorsVogel’s Model with Colors
Add colors to Vogel’s Model as shown here:

Vogel’s Model Variations AnimationVogel’s Model Variations Animation
Vogel’s Model uses Golden Angle as spacing between two dots. Vary this spacing number around the Golden Angle and see what the model looks like.

Vogel’s ModelVogel’s Model
Vogel’s model is closely related to the Fermat’s Spiral. Instead of continuously drawing the spiral curve, Vogel’s model draws dot in constant spacing. The constant space used in Vogel’s model
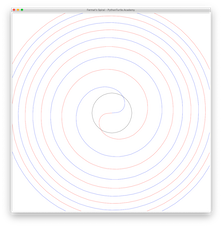
Fermat’s SpiralFermat’s Spiral
In a previous project, you drew Archimedean Spiral, in which radius increase linearly with the angle. In Fermat’s spiral, radius increases in proportion to the square root of the angle.
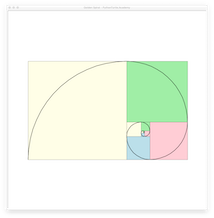
Golden SpiralGolden Spiral
In style similar to Fibonacci Spiral, draw the following Golden Spiral. Unlike Fibonacci tiling, the ratio between to successive squares is strictly golden ratio (1.61803398875). Please note that Golden Spiral

Fibonacci vs Golden Ratio TilingFibonacci vs Golden Ratio Tiling
Draw Fibonacci tiling and Golden Ratio Tiling in one canvas. Which one is Golden Ratio Tiling?

Golden Ratio TilingGolden Ratio Tiling
Golden Ratio is a number fib(n+1)/fib(n) will converge to, where fib(n) represents n-th fibonacci number. The value is (1+sqrt(5))/2 ≈ 1.61803398875. In similar style to fibonacci tiling, draw a golden