Tutorial: Conway’s Game of Life with Python Turtle

In this tutorial, we are you going show how to implement Conway’s Game of Life simulation with Python Turtle.

Step 1. Drawing The Grid

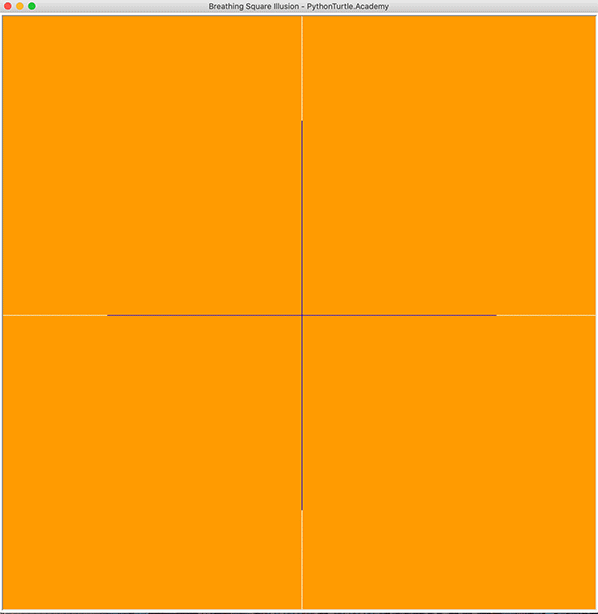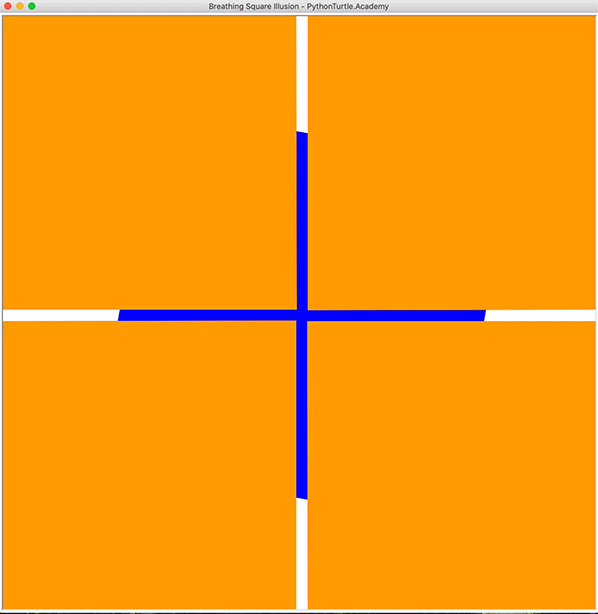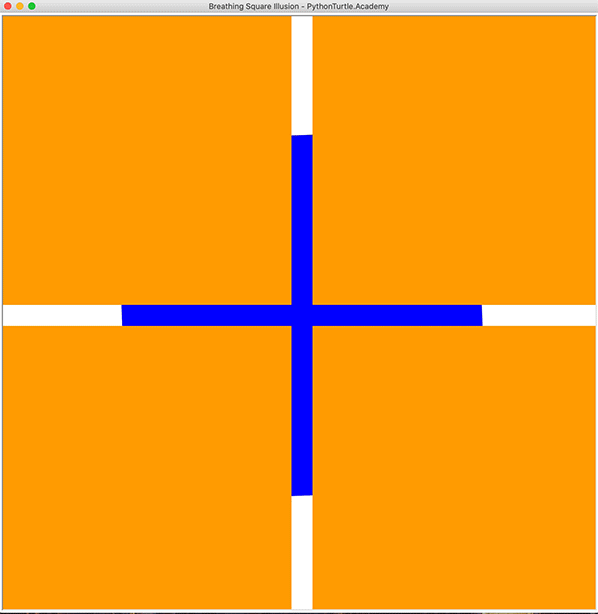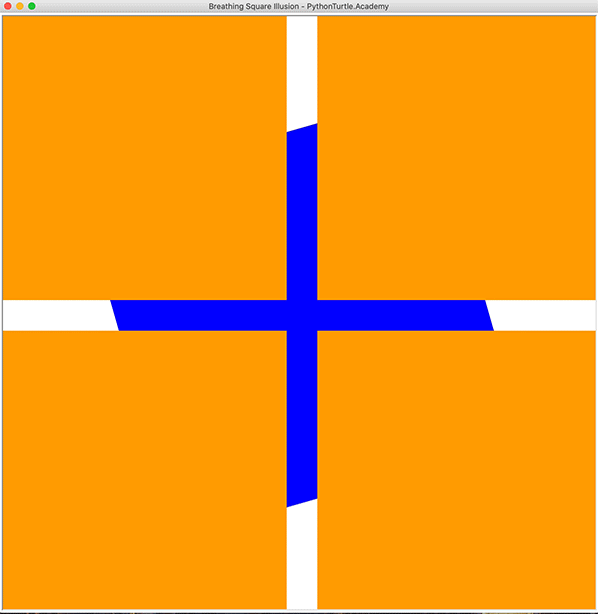
This step should be straightforward. We just need n horizontal and n vertical lines centered in the screen. The following is the code snippet that draws the grid.

screen=turtle.Screen()
turtle.setup(1000,1000)
turtle.title("Conway's Game of Life - PythonTurtle.Academy")
turtle.hideturtle()
turtle.speed(0)
turtle.tracer(0,0)

n = 50 # nxn grid
def draw_line(x1,y1,x2,y2): # this function draw a line between x1,y1 and x2,y2
    turtle.up()
    turtle.goto(x1,y1)
    turtle.down()
    turtle.goto(x2,y2)
    
def draw_grid(): # this function draws nxn grid
    turtle.pencolor('gray')
    turtle.pensize(3)
    x = -400
    for i in range(n+1):
        draw_line(x,-400,x,400)
        x += 800/n
    y = -400
    for i in range(n+1):
        draw_line(-400,y,400,y)
        y += 800/n

draw_grid()
screen.update()

It should a grid like the following picture:

Step 2: Creating Life

We need data structure to store the lives in the n x n cells. The natural data structure for this purpose is a list of lists. We are going to use value 1 to represent ‘life’ and 0 to represent ‘no life’. The lives in cells will be randomly generated with 1/7 probability of having life. The following is the code snippet that creates and initializes lives:

life = list() # create an empty list
def init_lives():
    for i in range(n):
        liferow = [] # a row of lives
        for j in range(n):
            if random.randint(0,7) == 0: # 1/7 probability of life
                liferow.append(1) # 1 means life
            else:
                liferow.append(0) # 0 means no life
        life.append(liferow) # add a row to the life list -> life is a list of list

Step 3: Displaying Life in Cells

The next task is to draw live cells in the grid. We will create and use a new turtle called lifeturtle to draw the live cells. Because cells can become alive or dead, we need to erase them and redraw in each cycle. However, there is no need to erase the grid. By just clearing the lifeturtle, there is no need to redraw the grid. The following is complete code for the first 3 steps.

import turtle
import random

screen=turtle.Screen()
turtle.setup(1000,1000)
turtle.title("Conway's Game of Life - PythonTurtle.Academy")
turtle.hideturtle()
turtle.speed(0)
turtle.tracer(0,0)

lifeturtle = turtle.Turtle() # turtle for drawing life
lifeturtle.up()
lifeturtle.hideturtle()
lifeturtle.speed(0)
lifeturtle.color('black')

n = 50 # nxn grid
def draw_line(x1,y1,x2,y2): # this function draw a line between x1,y1 and x2,y2
    turtle.up()
    turtle.goto(x1,y1)
    turtle.down()
    turtle.goto(x2,y2)
    
def draw_grid(): # this function draws nxn grid
    turtle.pencolor('gray')
    turtle.pensize(3)
    x = -400
    for i in range(n+1):
        draw_line(x,-400,x,400)
        x += 800/n
    y = -400
    for i in range(n+1):
        draw_line(-400,y,400,y)
        y += 800/n

life = list() # create an empty list
def init_lives():
    for i in range(n):
        liferow = [] # a row of lives
        for j in range(n):
            if random.randint(0,7) == 0: # 1/7 probability of life
                liferow.append(1) # 1 means life
            else:
                liferow.append(0) # 0 means no life
        life.append(liferow) # add a row to the life list -> life is a list of list

def draw_square(x,y,size): # draws a filled square 
    lifeturtle.up()
    lifeturtle.goto(x,y)
    lifeturtle.down()
    lifeturtle.seth(0)
    lifeturtle.begin_fill()
    for i in range(4):
        lifeturtle.fd(size)
        lifeturtle.left(90)
    lifeturtle.end_fill()

def draw_life(x,y): # draws life in (x,y)
    lx = 800/n*x - 400 # converts x,y to screen coordinate 
    ly = 800/n*y - 400
    draw_square(lx+1,ly+1,800/n-2)

def draw_all_life(): # draws all life
    global life
    for i in range(n):
        for j in range(n):
            if life[i][j] == 1: draw_life(i,j) # draw live cells

draw_grid()
init_lives()
draw_all_life()
screen.update()

It should draw a shape like the following image:

Step 4: Updating Life Forever

The next step is to update the life based on the Conway’s Rule:

1. If a cell with fewer than two or more than three live neighbors dies because of underpopulation or overpopulation.
2. If a live cell has two or three live neighbors, the cell survives to the next generation.
3. If a dead cell has exactly three live neighbors, it becomes alive.

We will create a function update_life() that will update the cells based on these rules. Then we will call this function again with the Turtle’s timer event. The following is the complete code for animating the Conway’s Game of Life:

import turtle
import random
import copy

screen=turtle.Screen()
turtle.setup(1000,1000)
turtle.title("Conway's Game of Life - PythonTurtle.Academy")
turtle.hideturtle()
turtle.speed(0)
turtle.tracer(0,0)

lifeturtle = turtle.Turtle() # turtle for drawing life
lifeturtle.up()
lifeturtle.hideturtle()
lifeturtle.speed(0)
lifeturtle.color('black')

n = 50 # nxn grid
def draw_line(x1,y1,x2,y2): # this function draw a line between x1,y1 and x2,y2
    turtle.up()
    turtle.goto(x1,y1)
    turtle.down()
    turtle.goto(x2,y2)
    
def draw_grid(): # this function draws nxn grid
    turtle.pencolor('gray')
    turtle.pensize(3)
    x = -400
    for i in range(n+1):
        draw_line(x,-400,x,400)
        x += 800/n
    y = -400
    for i in range(n+1):
        draw_line(-400,y,400,y)
        y += 800/n

life = list() # create an empty list
def init_lives():
    for i in range(n):
        liferow = [] # a row of lives
        for j in range(n):
            if random.randint(0,7) == 0: # 1/7 probability of life
                liferow.append(1) # 1 means life
            else:
                liferow.append(0) # 0 means no life
        life.append(liferow) # add a row to the life list -> life is a list of list

def draw_square(x,y,size): # draws a filled square 
    lifeturtle.up()
    lifeturtle.goto(x,y)
    lifeturtle.down()
    lifeturtle.seth(0)
    lifeturtle.begin_fill()
    for i in range(4):
        lifeturtle.fd(size)
        lifeturtle.left(90)
    lifeturtle.end_fill()

def draw_life(x,y): # draws life in (x,y)
    lx = 800/n*x - 400 # converts x,y to screen coordinate 
    ly = 800/n*y - 400
    draw_square(lx+1,ly+1,800/n-2)

def draw_all_life(): # draws all life
    global life
    for i in range(n):
        for j in range(n):
            if life[i][j] == 1: draw_life(i,j) # draw live cells

def num_neighbors(x,y): # computes the number of life neighbours for cell[x,y]
    sum = 0
    for i in range(max(x-1,0),min(x+1,n-1)+1):
        for j in range(max(y-1,0),min(y+1,n-1)+1):
            sum += life[i][j]
    return sum - life[x][y]
        
def update_life(): # update life for each cycle
    global life 
    newlife = copy.deepcopy(life) # make a copy of life
    for i in range(n):
        for j in range(n):
            k = num_neighbors(i,j)
            if k < 2 or k > 3:
                newlife[i][j] = 0
            elif k == 3:
                newlife[i][j] = 1
    life = copy.deepcopy(newlife) # copy back to life
    lifeturtle.clear() # clears life in previous cycle
    draw_all_life()
    screen.update() 
    screen.ontimer(update_life,200) # update life every 0.2 second

draw_grid()
init_lives()
update_life()

Related Projects:

• Projects with similar difficulty
• Games
• Animation