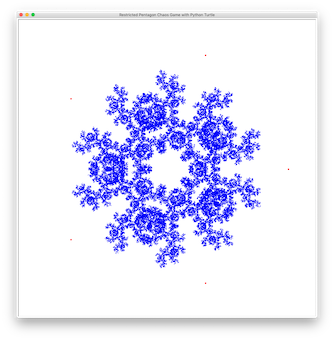
In a previous project, you drew a Sierpinski Triangle with Chaos Game. Instead of a triangle, use five points of a pentagon as the target points and play the chaos game. There is restriction: you can’t choose the same direction as the last move. It should draw something like this after 100,000 iterations:

Solution:
import turtle
import random
import math
screen = turtle.Screen()
screen.title('Restricted Pentagon Chaos Game with Python Turtle')
screen.setup(1000,1000)
screen.tracer(0,0)
turtle.hideturtle()
turtle.speed(0)
turtle.up()
m=5
angle = 0
V = []
for i in range(m):
p = (400*math.cos(angle),400*math.sin(angle))
V.append(p)
angle += math.pi*2/m
for v in V:
turtle.goto(v)
turtle.dot('red')
n = 100000 # number of points to draw
p = (random.uniform(-200,200),random.uniform(-200,200)) # random starting point
t = turtle.Turtle()
t.up()
t.hideturtle()
lastr = r = -1
for i in range(n):
t.goto(p)
t.dot(2,'blue')
while r == lastr:
r = random.randrange(len(V)) # pick a random vertex
lastr = r
p = ((V[r][0]+p[0])/2,(V[r][1]+p[1])/2) # go to mid point between the random vertex and point
if i % 1000 == 0: # update for every 1000 moves, this part is for performance reason only
t = turtle.Turtle() # use new turutle
t.up()
t.hideturtle()
screen.update()