Golden Ratio is a number fib(n+1)/fib(n) will converge to, where fib(n) represents n-th fibonacci number. The value is (1+sqrt(5))/2 ≈ 1.61803398875. In similar style to fibonacci tiling, draw a golden
Author: J & J Coding Adventure
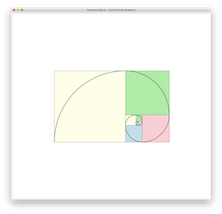
Fibonacci SpiralFibonacci Spiral
Continue with Fibonacci Tiling project to draw a curve called Fibonacci Spiral.
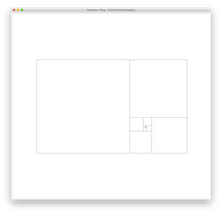
Fibonacci TilingFibonacci Tiling
Fibonacci sequence is a series of numbers with each number being the sum of previous two numbers. The first numbers are 1, 1. Here is the first 10 numbers in
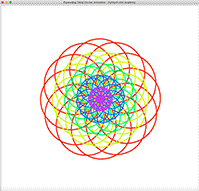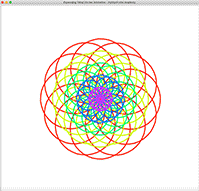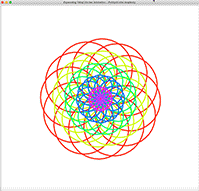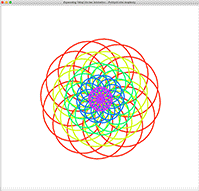
Expanding Tilted Circles AnimatedExpanding Tilted Circles Animated
You drew an Expanding Tilted Circles in a previous project. Animate by rotating these circles with circles inside moving faster than circles outside.

Expanding Tilted CirclesExpanding Tilted Circles
You drew 60 tilted circles. Now draw fewer circles but with circles of expanding sizes. You can also add color to make it look better.
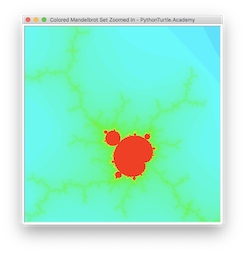
Zooming into Mandelbrot SetZooming into Mandelbrot Set
Let’s zoom into Mandelbrot Set and see what details it has. Each picture shows the x,y coordinates of the center and the radius.
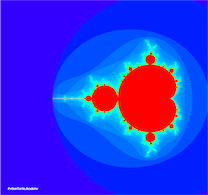
Colored Mandelbrot SetColored Mandelbrot Set
Continuing from Mandelbrot Set project, use colorsys library to set the hue based on the number of iterations needed to go outside the boundary. The result can be an amazingly

Mandelbrot SetMandelbrot Set
Mandelbrot Set is a very intriguing and complex shape. Although it doesn’t appear to be recursive, it has part that contains the main shape shown here. You will need to
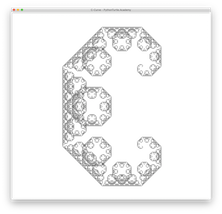
Lévy C CurveLévy C Curve
Although looking very different, Lévy C Curve’s construction is almost identical to the Jurassic Park Curve. The following is demo of recursive steps of drawing this curve.

Four Jurassic Park DragonsFour Jurassic Park Dragons
Jurassic Park Dragons can align perfectly. Draw four dragons as shown here. Related Projects: Jurassic Park Dragon Colored Jurassic Park Dragon

