Cesàro (Torn Squares) Fractal with Python Turtle (Source Code)

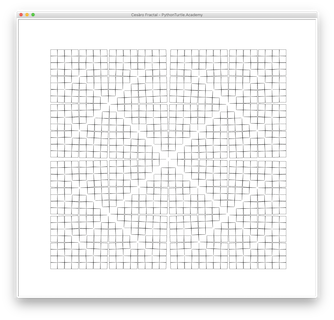
Cesàro (Torn Squares) Fractal is a variation of Koch Snowflake. In Cesàro Fractal the degree to turn can vary from 60 degrees to 90 degrees. Koch Snowflake line only curves 60 degrees.

Instead of choosing a degree to turn, Cesàro Fractal is easier to implement by setting the ratio of original length for each of the 4 segments. For Koch snowflake, the ratio is 1/3. For Cesàro Fractal the ratio can range from 1/3 to 1/2. The following is the Cesàro Fractal with different ratios:

Source Code:

import turtle
import math

screen = turtle.Screen()
screen.title('Cesàro (Torn Square) Fractal - PythonTurtle.Academy')
screen.setup(1000,1000)
screen.setworldcoordinates(-1000,-1000,1000,1000)
screen.tracer(0,0)
turtle.speed(0)
turtle.hideturtle()
turtle.fillcolor('blue')

# ratio is between [1/3, 1/2)
def Cesàro(x1,y1,x2,y2,ratio):
    dist = ((x2-x1)**2+(y2-y1)**2)**0.5
    if dist<50:
        turtle.goto(x2,y2)
        return
    direction = math.atan2(y2-y1,x2-x1)
    px1, py1 = x1+dist*ratio*math.cos(direction), y1+dist*ratio*math.sin(direction)    
    px3, py3 = x1+dist*(1-ratio)*math.cos(direction), y1+dist*(1-ratio)*math.sin(direction)
    ptx, pty = (px1+px3)/2, (py1+py3)/2
    d = ((dist*ratio)**2 - (dist*(1-2*ratio)/2)**2)**0.5
    px2, py2 = ptx+d*math.cos(direction+math.radians(90)), pty+d*math.sin(direction+math.radians(90))
        
    Cesàro(x1,y1,px1,py1,ratio)
    Cesàro(px1,py1,px2,py2,ratio)
    Cesàro(px2,py2,px3,py3,ratio)
    Cesàro(px3,py3,x2,y2,ratio)

ratio = 0.49
turtle.up()
turtle.goto(-800,800)
turtle.down()
Cesàro(-800,800,-800,-800,ratio)
Cesàro(-800,-800,800,-800,ratio)
Cesàro(800,-800,800,800,ratio)
Cesàro(800,800,-800,800,ratio)

screen.update()