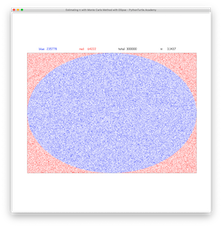
Monte Carlo Methods are interesting algorithms that rely on random sampling to obtain numeric result (Wikipedia). Since today is Pi Day, we are going to design a Monte Carol method to estimate the value of π. In a previous project, we estimated π with Monte Carlo Method with a quarter circle. This time, we are going to estimate π with an ellipse.
Draw a 600*sqrt(2) by 600 rectangle on canvas. Randomly generate a coordinate (x,y) that falls inside this rectangle and draw a small point (using Turtle’s dot() function) on this position. If the sum of distance of this point to two focal points (-300,0) and (300,0) is less than 600*sqrt(2), draw this point with blue color. If the distance equals to 600*sqrt(2), draw this point with blue or red color with 50% chance each. Otherwise, draw this point with red color. Keep generating this point a lot times as you keep count of red points and blue points.
The area of an ellipse is πab where a, b are two radii of the ellipse. The area of our ellipse is π*300*sqrt(2)*300. The are of the bounding rectangle is 600*sqrt(2)*600. So, the ratio blue over the total number points times 4 should estimate the value of π.