Pentaflake Fractal with Python Turtle (Source Code)

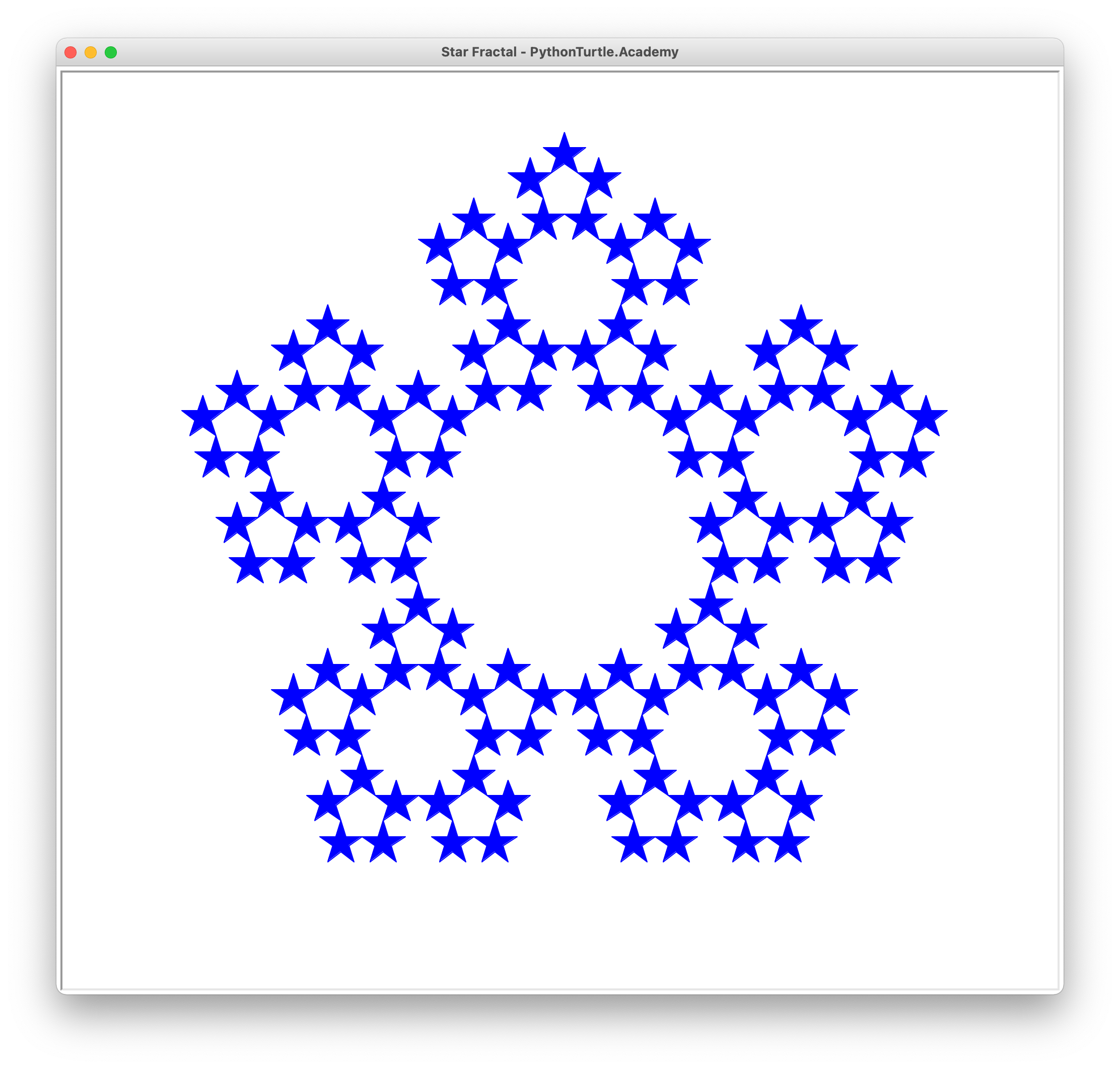
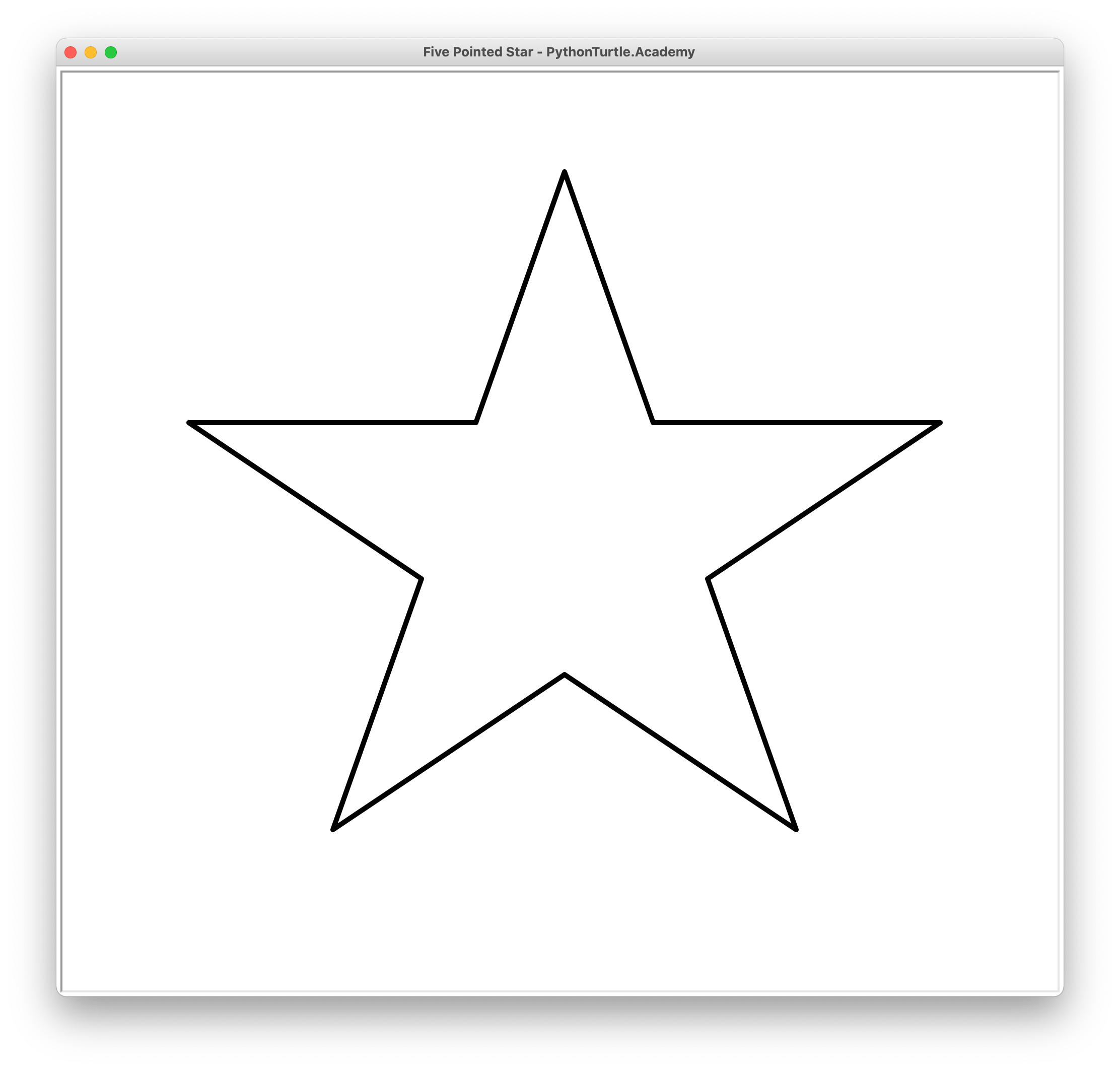
Draw the shown pentaflake fractal shape. The following figures show pentaflakes in different recursion depths.

Source Code:

import turtle
import math

screen = turtle.Screen()
screen.title('Pentaflake Fractal - PythonTurtle.Academy')
screen.setup(1000,1000)
screen.setworldcoordinates(-1000,-1000,1000,1000)
turtle.speed(0)
turtle.hideturtle()
screen.tracer(0,0)
turtle.fillcolor('dark cyan')

def pentagon(x,y,r,direction,pencolor): #x,y is the center
    turtle.up()
    turtle.goto(x,y)
    turtle.seth(direction)
    turtle.fd(r)
    turtle.left(126)
    turtle.down()
    turtle.pencolor(pencolor)
    turtle.begin_fill()
    for _ in range(5):
        turtle.fd(2*r*math.sin(math.radians(36)))
        turtle.left(72)
    turtle.end_fill()
    
def pentaflake(x,y,r,direction,n,pencolor='dark cyan'):
    if n==0:
        pentagon(x,y,r,direction,pencolor)
        return

    r2 = r/(1+2*math.cos(math.radians(36)))
    d = 2*r2*math.cos(math.radians(36))
    for _ in range(5):
        x2,y2 = x+d*math.cos(math.radians(direction)),y+d*math.sin(math.radians(direction))
        pentaflake(x2,y2,r2,direction,n-1)
        direction += 72
    pentaflake(x,y,r2,direction+180,n-1,'dark green')
    
pentaflake(0,0,1000,90,0,'dark green')
screen.update()