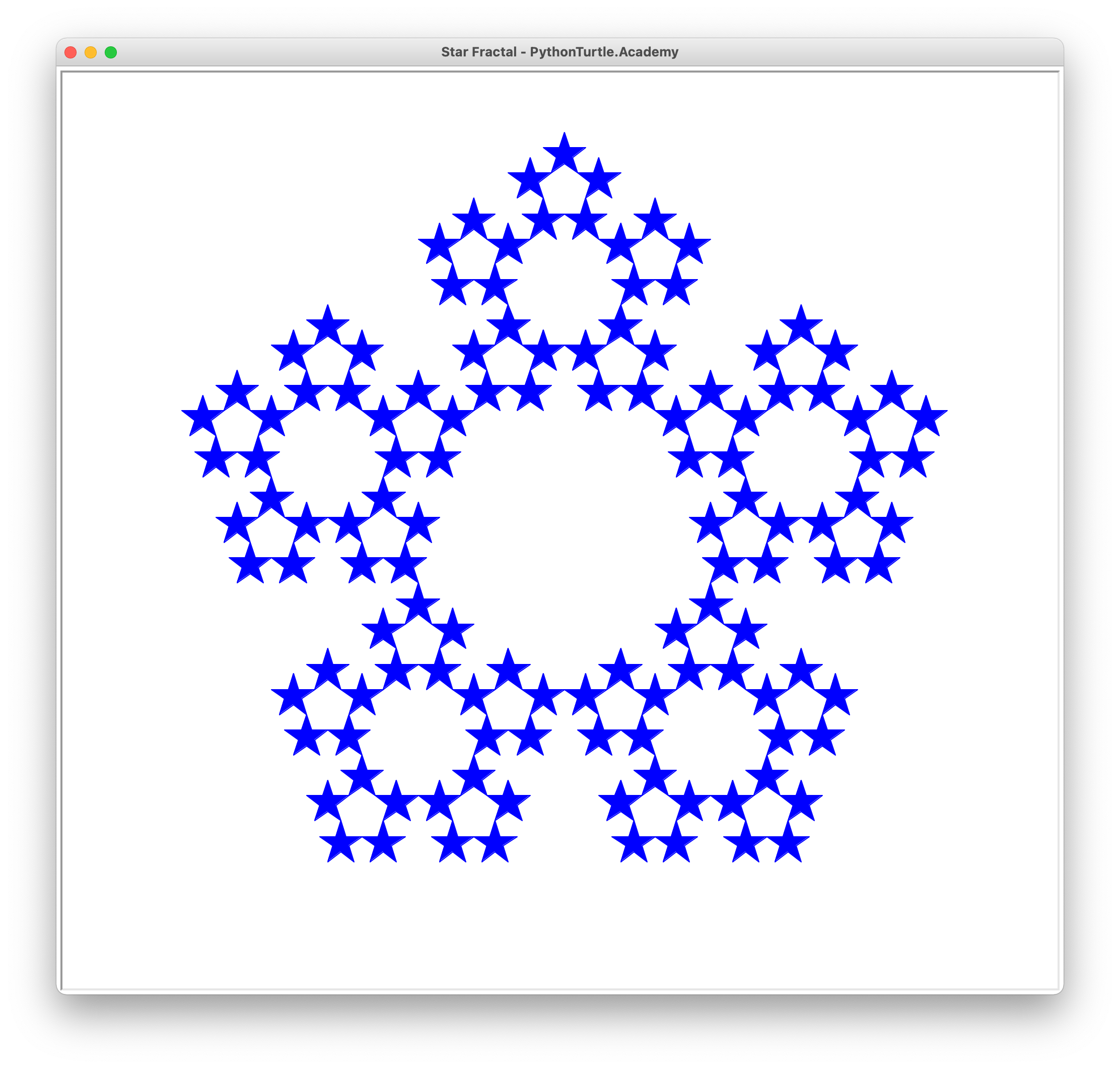
Draw the following fractal made up with stars. You may need to use recursion and trigonometry to do this project.

The following figures show star fractal with different recursion depths (from depth 0 to depth 4)




Solution
It is very helpful to make a function that draws star at any given center and size. The following code is the function that does the work. It also can draw filled stars given pen color and fill color.
def star(x,y,length,penc,fillc):
turtle.up()
turtle.goto(x,y)
turtle.seth(90)
turtle.fd(length)
turtle.seth(180+36/2)
L = length*math.sin(36*math.pi/180)/math.sin(54*math.pi/180)
turtle.seth(180+72)
turtle.down()
turtle.fillcolor(fillc)
turtle.pencolor(penc)
turtle.begin_fill()
for _ in range(5):
turtle.fd(L)
turtle.right(72)
turtle.fd(L)
turtle.left(144)
turtle.end_fill()
The next step is to define a recursive function that draws the star fractal. One way to stop the recursion function is to set the depth limit. In each recursive call decrement the depth limit by 1. The base condition of the recursive call is when the depth limit is 0. In this case, just draw a star by calling the function we defined above. It requires some trigonometry to figure out the centers and the size of 5 star fractals relative to the current center and size. The following code is the recursive function:
def star_fractal(x,y,length,penc,fillc,n):
if n==0:
star(x,y,length,penc,fillc)
return
length2 = length/(1+(math.sin(18*math.pi/180)+1)/math.sin(54*math.pi/180))
L = length-length2-length2*math.sin(18*math.pi/180)/math.sin(54*math.pi/180)
for i in range(5):
star_fractal(x+math.cos((90+i*72)*math.pi/180)*(length-length2),
y+math.sin((90+i*72)*math.pi/180)*(length-length2),
length2,penc,fillc,n-1)
The following is the complete code:
import turtle
import math
screen = turtle.Screen()
screen.title('Star Fractal - PythonTurtle.Academy')
screen.setup(1000,1000)
screen.tracer(0,0)
turtle.hideturtle()
turtle.speed(0)
def star(x,y,length,penc,fillc):
turtle.up()
turtle.goto(x,y)
turtle.seth(90)
turtle.fd(length)
turtle.seth(180+36/2)
L = length*math.sin(36*math.pi/180)/math.sin(54*math.pi/180)
turtle.seth(180+72)
turtle.down()
turtle.fillcolor(fillc)
turtle.pencolor(penc)
turtle.begin_fill()
for _ in range(5):
turtle.fd(L)
turtle.right(72)
turtle.fd(L)
turtle.left(144)
turtle.end_fill()
def star_fractal(x,y,length,penc,fillc,n):
if n==0:
star(x,y,length,penc,fillc)
return
length2 = length/(1+(math.sin(18*math.pi/180)+1)/math.sin(54*math.pi/180))
L = length-length2-length2*math.sin(18*math.pi/180)/math.sin(54*math.pi/180)
for i in range(5):
star_fractal(x+math.cos((90+i*72)*math.pi/180)*(length-length2),
y+math.sin((90+i*72)*math.pi/180)*(length-length2),
length2,penc,fillc,n-1)
star_fractal(0,0,400,'blue','blue',3)
screen.update()