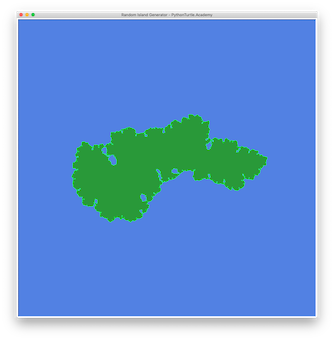
In this tutorial we are going to show how to draw random islands with Python Turtle. The idea is similar to the Koch Snowflake project with added randomness. Instead of sub-dividing a line into 4 equal segments of 1/3 of the original length, we will simplify it by dividing a line into two segments with the sum slightly larger than the original line.
The following is the code snippet that recursively subdivides a line segment into two segments each has length: 0.53*(original length). So, each subdivision will increase the length by 6%.
def draw_line(x1,y1,x2,y2): # function to draw line
turtle.up()
turtle.goto(x1,y1)
turtle.down()
turtle.goto(x2,y2)
def dist(p1,p2): # Euclidean distance betwen p1 and p2
return ((p1[0]-p2[0])**2 + (p1[1]-p2[1])**2)**0.5
def shoreline(x1,y1,x2,y2,ratio): # recurisve function to draw the shoreline
L = dist((x1,y1),(x2,y2))
if L <= 1: # distance is short enough, directly draw the line
draw_line(x1,y1,x2,y2)
return
alpha = math.acos(1/(2*ratio)) # The angle to turn for subdivided segments
beta = math.atan2(y2-y1,x2-x1) # The angle between two end points
x3 = x1 + L*ratio*math.cos(alpha+beta) # coordinates of the mid points between two segments
y3 = y1 + L*ratio*math.sin(alpha+beta)
shoreline(x1,y1,x3,y3,ratio) # do this recursively on each segment
shoreline(x3,y3,x2,y2,ratio)
turtle.tracer(0,0)
turtle.bgcolor('royal blue')
turtle.pencolor('green')
shoreline(-300,0,300,0,0.53) # call recursion
turtle.update()
The curve above looks too perfect to be a shoreline of an island. Let’s add some randomness to the process. We can randomize the the ratio (0.55) to a range of ratios. We can also randomize the point of division from middle to somewhere left or somewhere right of it. To implement this, we need to use ellipse. Two end points of a line are the focal points of the ellipse, and the sum of distance from any point on the ellipse to the focal points should be a constant, which is 2*ratio*(length of line). The following is the code snippet for part we described above:
def draw_line(x1,y1,x2,y2): # function to draw line
turtle.up()
turtle.goto(x1,y1)
turtle.down()
turtle.goto(x2,y2)
def dist(p1,p2): # Euclidean distance betwen p1 and p2
return ((p1[0]-p2[0])**2 + (p1[1]-p2[1])**2)**0.5
def shoreline(x1,y1,x2,y2,ratio): # recurisve function to draw the shoreline
L = dist((x1,y1),(x2,y2))
if L <= 1: # distance is short enough, directly draw the line
draw_line(x1,y1,x2,y2)
return
rs = ratio + random.uniform(-0.1,0.1) # let ratio flucuate slightly around the chosen value
rs = max(0.5,rs) # make sure ratio stays at least half of the length
midx = (x1+x2)/2 # center of ellipse
midy = (y1+y2)/2
rx = L/2 + (2*rs-1)/2*L # width of ellipse
ry = ((L*rs)**2 - (L/2)**2)**0.5 # height of ellipse
theta = math.atan2(y2-y1,x2-x1) # the tilt angle of ellipse
alpha = random.uniform(math.pi*0.3,math.pi*0.7) # flucuate around math.pi/2
x3 = rx*math.cos(alpha)*math.cos(theta) - ry*math.sin(alpha)*math.sin(theta) + midx # parametric equation for ellipse
y3 = rx*math.cos(alpha)*math.sin(theta) + ry*math.sin(alpha)*math.cos(theta) + midy
shoreline(x1,y1,x3,y3,ratio) # do this recursively on each segment
shoreline(x3,y3,x2,y2,ratio)
turtle.tracer(0,0)
turtle.bgcolor('royal blue')
turtle.pencolor('green')
shoreline(-300,0,300,0,0.55) # call recursion
turtle.update()The code above should draw something looks random:

The rest is easy: Just draw a line backward and fill the whole thing. The following is the complete code for drawing a random island shape.
import turtle
import math
import random
turtle.setup(1000,1000)
turtle.title("Random Island Generator - PythonTurtle.Academy")
turtle.speed(0)
turtle.hideturtle()
def draw_line(x1,y1,x2,y2): # function to draw line
turtle.up()
turtle.goto(x1,y1)
turtle.down()
turtle.goto(x2,y2)
def dist(p1,p2): # Euclidean distance betwen p1 and p2
return ((p1[0]-p2[0])**2 + (p1[1]-p2[1])**2)**0.5
def shoreline(x1,y1,x2,y2,ratio): # recurisve function to draw the shoreline
L = dist((x1,y1),(x2,y2))
if L <= 1: # distance is short enough, directly draw the line
draw_line(x1,y1,x2,y2)
return
rs = ratio + random.uniform(-0.1,0.1) # let ratio flucuate slightly around the chosen value
rs = max(0.5,rs) # make sure ratio stays at least half of the length
midx = (x1+x2)/2 # center of ellipse
midy = (y1+y2)/2
rx = L/2 + (2*rs-1)/2*L # width of ellipse
ry = ((L*rs)**2 - (L/2)**2)**0.5 # height of ellipse
theta = math.atan2(y2-y1,x2-x1) # the tilt angle of ellipse
alpha = random.uniform(math.pi*0.3,math.pi*0.7) # flucuate around math.pi/2
x3 = rx*math.cos(alpha)*math.cos(theta) - ry*math.sin(alpha)*math.sin(theta) + midx # parametric equation for ellipse
y3 = rx*math.cos(alpha)*math.sin(theta) + ry*math.sin(alpha)*math.cos(theta) + midy
shoreline(x1,y1,x3,y3,ratio) # do this recursively on each segment
shoreline(x3,y3,x2,y2,ratio)
turtle.tracer(0,0)
turtle.bgcolor('royal blue')
turtle.pencolor('green')
turtle.fillcolor('forest green')
turtle.begin_fill()
shoreline(-300,0,300,0,0.55) # call recursion
shoreline(300,0,-300,0,0.55) # call recursion
turtle.end_fill()
turtle.update()You can adjust the ratio value to draw different looking islands. The higher the ratio the crazier the shape of the island shape will look.