Game of SIM with Python Turtle (Source Code Included)

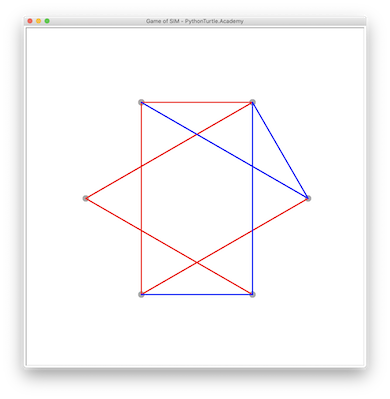
Game of SIM was invented in 1969 by Gustavus Simmons. In this two player (red and blue) game, each player takes turn to connect two vertices of a hexagon with the player’s color (either red or blue). The first player who draws all three sides of the triangle with the player’s color loses the game. There is always a winner for this game.

Write a Game of SIM with Python and Turtle graphics. Your game should be able to declare the winner when the game ends. You will need to use onclick() even of Turtle graphics.

Source Code:

import turtle
import math

screen = turtle.Screen()
screen.setup(800,800)
screen.title("Game of SIM - PythonTurtle.Academy")
screen.setworldcoordinates(-1.5,-1.5,1.5,1.5)
screen.tracer(0,0)
turtle.hideturtle()

def draw_dot(x,y,color):
    turtle.up()
    turtle.goto(x,y)
    turtle.color(color)
    turtle.dot(15)

def gen_dots():
    r = []
    for angle in range(0,360,60):
        r.append((math.cos(math.radians(angle)),math.sin(math.radians(angle))))
    return r

def draw_line(p1,p2,color):
    turtle.up()
    turtle.pensize(3)
    turtle.goto(p1)
    turtle.down()
    turtle.color(color)
    turtle.goto(p2)
    
def draw_board():
    global selection
    
    for i in range(len(dots)):
        if i in selection: draw_dot(dots[i][0],dots[i][1],turn)
        else: draw_dot(dots[i][0],dots[i][1],'dark gray')
        
def draw():
    draw_board()
    for i in range(len(red)):
        draw_line((math.cos(math.radians(red[i][0]*60)),math.sin(math.radians(red[i][0]*60))),\
                  (math.cos(math.radians(red[i][1]*60)),math.sin(math.radians(red[i][1]*60))),\
                  'red')
    for i in range(len(blue)):
         draw_line((math.cos(math.radians(blue[i][0]*60)),math.sin(math.radians(blue[i][0]*60))),\
                  (math.cos(math.radians(blue[i][1]*60)),math.sin(math.radians(blue[i][1]*60))),\
                  'blue')      
    screen.update()

def play(x,y):
    global selection,turn,red,blue
    
    for i in range(len(dots)):
        dist = (dots[i][0]-x)**2 + (dots[i][1]-y)**2
        if dist<0.001:
            if i in selection: selection.remove(i)
            else: selection.append(i)
            break
    if len(selection)==2:
        selection=(min(selection),max(selection))
        if selection not in red and selection not in blue:
            if turn=='red':
                red.append(selection)
            else:
                blue.append(selection)
            turn = 'red' if turn=='blue' else 'blue'
        selection = []
    draw()
    r = gameover(red,blue)
    if r!=0:
        screen.textinput('game over',r+' won!')
        turtle.bye()

def gameover(r,b):
    if len(r)<3: return 0
    r.sort()
    for i in range(len(r)-2):
        for j in range(i+1,len(r)-1):
            for k in range(j+1,len(r)):
                if r[i][0]==r[j][0] and r[i][1]==r[k][0] and r[j][1]==r[k][1]: return 'blue'
    if len(b)<3: return 0
    b.sort()
    for i in range(len(b)-2):
        for j in range(i+1,len(b)-1):
            for k in range(j+1,len(b)):
                if b[i][0]==b[j][0] and b[i][1]==b[k][0] and b[j][1]==b[k][1]: return 'red'
    return 0

selection = []
turn = 'red'
dots = gen_dots()
red = [ ]
blue = [ ]
draw()
screen.onclick(play)
turtle.mainloop()