Using the center coordinate and zoom factor to draw the following Mandelbrot Set visualizations.







Source Code:
from PIL import Image
import colorsys
import math
px, py = -0.7746806106269039, -0.1374168856037867 #Tante Renate
px, py, zoom = -0.74384935657398, -0.13170134084746293, 5788441.443619884
px, py, zoom = 2.613577e-1, -2.018128e-3, 3.354786e+3
px, py, zoom = -0.59990625, -0.4290703125, 1024
px, py, zoom = -1.038650e-1, -9.584393e-1, 1.674667e+5
px, py, zoom = -0.761574, -0.0847596, 78125
px, py, zoom = -1.62917,-0.0203968, 3125
px, py, zoom = -0.75,0,1
R = 3
max_iteration = 512
w, h = 1250,1250
mfactor = 1
def Mandelbrot(x,y,max_iteration,minx,maxx,miny,maxy):
zx = 0
zy = 0
RX1, RX2, RY1, RY2 = px-R/2, px+R/2,py-R/2,py+R/2
cx = (x-minx)/(maxx-minx)*(RX2-RX1)+RX1
cy = (y-miny)/(maxy-miny)*(RY2-RY1)+RY1
i=0
while zx**2 + zy**2 <= 4 and i < max_iteration:
temp = zx**2 - zy**2
zy = 2*zx*zy + cy
zx = temp + cx
i += 1
return i
def gen_Mandelbrot_image():
bitmap = Image.new("RGB", (w, h), "white")
pix = bitmap.load()
for x in range(w):
for y in range(h):
c=Mandelbrot(x,y,max_iteration,0,w-1,0,h-1)
v = c**mfactor/max_iteration**mfactor
hv = 0.67-v*2
#if hv<0: hv+=1
r,g,b = colorsys.hsv_to_rgb(hv,1,1-(v-0.1)**2/0.9**2)
r = min(255,round(r*255))
g = min(255,round(g*255))
b = min(255,round(b*255))
pix[x,y] = int(r) + (int(g) << 8) + (int(b) << 16)
bitmap.save("Mandelbrot_"+str(px)+"_"+str(py)+"_"+str(zoom)+".jpg")
bitmap.show()
R=3/zoom
gen_Mandelbrot_image()
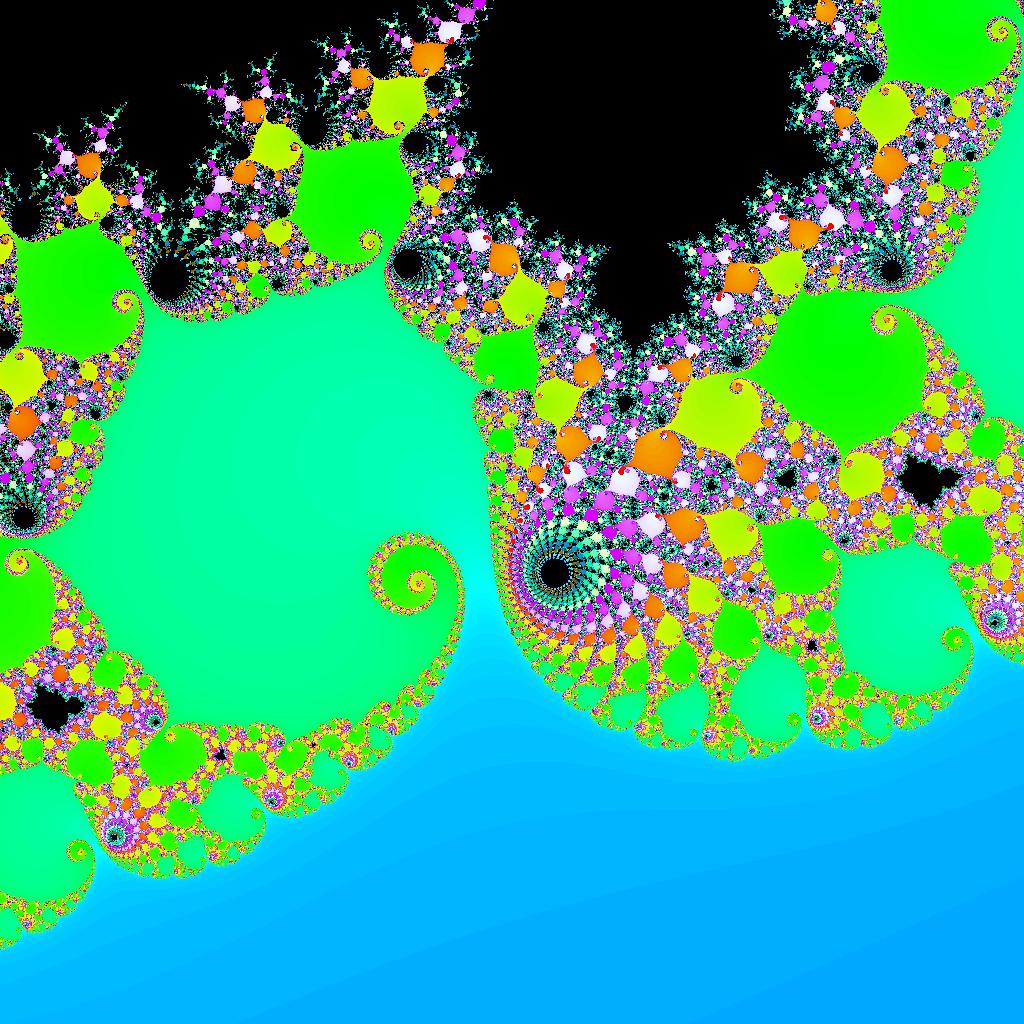

learning code for colour system great