Minkowski Island with Python Turtle (Source Code)

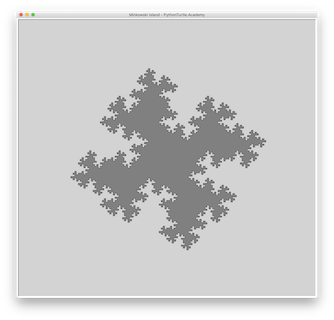
Minkowski Island is a fractal that is a variant to Koch snowflake. The following figures show Minkowski Island.

Source Code:

import turtle
import math

screen = turtle.Screen()
screen.title('Minkowski Island - PythonTurtle.Academy')
screen.setup(1000,1000)
screen.setworldcoordinates(-2000,-2000,2000,2000)
screen.tracer(0,0)
turtle.speed(0)
turtle.hideturtle()

def Minkowski(x1,y1,x2,y2,n):
    if n==0:
        turtle.goto(x2,y2)
        return
    dist = ((x2-x1)**2+(y2-y1)**2)**0.5
    direction = math.atan2(y2-y1,x2-x1)
    px1, py1 = x1+dist/4*math.cos(direction), y1+dist/4*math.sin(direction)
    px2, py2 = px1+dist/4*math.cos(direction+math.radians(90)), py1+dist/4*math.sin(direction+math.radians(90))
    px3, py3 = px2+dist/4*math.cos(direction), py2+dist/4*math.sin(direction)
    px4, py4 = px3+dist/4*math.cos(direction-math.radians(90)), py3+dist/4*math.sin(direction-math.radians(90))
    px5, py5 = px4+dist/4*math.cos(direction-math.radians(90)), py4+dist/4*math.sin(direction-math.radians(90))
    px6, py6 = px5+dist/4*math.cos(direction), py5+dist/4*math.sin(direction)
    px7, py7 = x1+3*dist/4*math.cos(direction), y1+3*dist/4*math.sin(direction)
        
    Minkowski(x1,y1,px1,py1,n-1)
    Minkowski(px1,py1,px2,py2,n-1)
    Minkowski(px2,py2,px3,py3,n-1)
    Minkowski(px3,py3,px4,py4,n-1)
    Minkowski(px4,py4,px5,py5,n-1)
    Minkowski(px5,py5,px6,py6,n-1)
    Minkowski(px6,py6,px7,py7,n-1)
    Minkowski(px7,py7,x2,y2,n-1)

turtle.up()
turtle.goto(-800,-800)
turtle.down()
n=3
screen.bgcolor('light gray')
turtle.fillcolor('gray')
turtle.begin_fill()
Minkowski(-800,-800,-800,800,n)
Minkowski(-800,800,800,800,n)
Minkowski(800,800,800,-800,n)
Minkowski(800,-800,-800,-800,n)
turtle.end_fill()
screen.update()